¿Qué son los números naturales?
Para negociar y ordenar cosas, el hombre tuvo la necesidad de representar las cantidades de lo que tenía para saber con qué contaba exactamente. De ahí surgió la necesidad de crear símbolos que representaran esas cantidades.
Por ejemplo, si alguien sabía cuántas gallinas tenía, podría establecer del mismo modo la cantidad de días que podría alimentar a su familia.

A partir de esta necesidad el hombre crea lo que hoy conocemos como números naturales. Estos son los primeros que surgen en las distintas civilizaciones debido a que contar y ordenar elementos son las tareas más elementales en el tratamiento de las cantidades.
Los números naturales son aquellos símbolos que nos permiten representar la cantidad de elementos que tiene un conjunto.

Debido a la importancia de este conjunto de números se creó un símbolo especial para identificarlo, usaremos la letra N para representar el conjunto de los números naturales; así, cuando veas esta N en un libro de matemáticas, o en alguna clase, sabrás a qué se refiere.
¿Te has preguntado cuál es el último número natural? No hay, sencillamente no existe un número natural que sea más grande que todos los demás, cada vez que pienses en uno, podrás encontrar muchos que sean mayores que él. Como no terminan nunca, decimos que N es un conjunto infinito.
¿Qué caracteriza a los números naturales?
No podemos pasar por alto el hecho de que una de las principales señas de identidad o características que definen a los citados números naturales es el hecho de que los mismos están ordenados. De esta manera, gracias a dicho orden se pueden comparar los números entre sí. Así, por ejemplo, podríamos subrayar en ese sentido que el 8 es mayor que el 3 o que el 1 es menor que el 6.
De la misma forma, otra de las cualidades que diferencian a los citados números que nos ocupan es el hecho de que son ilimitados. Eso lo que significa es que siempre que le sume el 1 a uno de ellos nos dará lugar a otro número natural absolutamente diferente.
Por todo ello, nos encontramos con el hecho de que estos números se pueden representar en una línea recta y siempre se ordenan de menor a mayor. Así, una vez que señalemos en aquella el 0 procederemos a establecer el resto de número (1, 2, 3…) a la derecha de aquel.
Los números naturales pertenecen al conjunto de los números enteros positivos: no tienen decimales, no son fraccionarios y se encuentran a la derecha del cero en la recta real. Son infinitos, ya que incluyen a todos los elementos de una sucesión (1, 2, 3, 4, 5…).
Sin embargo, los números naturales constituyen un conjunto cerrado para las operaciones de suma y multiplicación ya que, al operar con cualquiera de sus elementos, el resultado siempre será un número natural: 5+4=9, 8×4=32. No ocurre lo mismo, en cambio, con la resta (5-12= -7) o con la división (4/3=1,33).
Propiedades del conjunto de los números naturales
Los números naturales poseen propiedades únicas que los diferencian de los demás conjuntos numéricos, te invitamos a conocerlas.
Operaciones en el conjunto de los números naturales

Los números naturales son aquellos que nos permiten contar los elementos de un determinado conjunto. Gracias a esto, cuando realizamos operaciones con ellos, los resultados pueden ser o no números naturales.
Si sumamos dos números naturales, el resultado siempre será otro número natural. Lo mismo ocurre cuando multiplicamos, pero cuando restamos dos números naturales el resultado no siempre será otro número natural, lo mismo ocurre con la división.
Por ejemplo, intenta restar menos , ¿crees que es posible representar el resultado de esta operación con algún número natural? Debido a lo anterior consideramos sobre el conjunto de los números naturales solo dos operaciones: la suma y la multiplicación. Si quieres aprender más sobre ellas visita nuestros cursos Suma y Multiplicación.
El primer natural
Como hemos dicho que los naturales son los números sirven para representar la cantidad de elementos que tiene un determinado conjunto, tomaremos el conjunto de los naturales o ℕ a partir del , pues este número representa la cantidad de elementos que tiene el conjunto vacío.

El sucesor de un número natural
Otra propiedad importante de este conjunto de números es que cada uno de sus elementos tiene un sucesor. Es decir, si tomamos como referencia determinado número natural, podemos saber cual es el siguiente y tener la certeza que entre el número y su siguiente no habrá ningún otro. Este número es llamado sucesor. Si por ejemplo tomamos como referencia el , sabemos su sucesor será el y entre estos dos números no encontraremos ningún otro. ¡Aunque te parezca increíble no todos los conjuntos numéricos cumplen esta sencilla propiedad!
Orden de los números naturales
En su función de representar cantidades, existen unos números naturales que representan más que otros. Decimos entonces que hay números naturales mayores o menores que otros, esta relación es llamada orden.
Para representar que un número es mayor que otro usaremos el símbolo “mayor que”: , de la siguiente manera: ubicamos el número mayor al lado abierto del símbolo , el menor lo ubicamos al otro lado.
Tomemos como ejemplo el y el . Sabemos desde nuestra infancia que el representa una mayor cantidad de elementos que el . Debemos escribir por lo tanto . Esta expresión debe ser leída como “cinco es mayor que tres”.
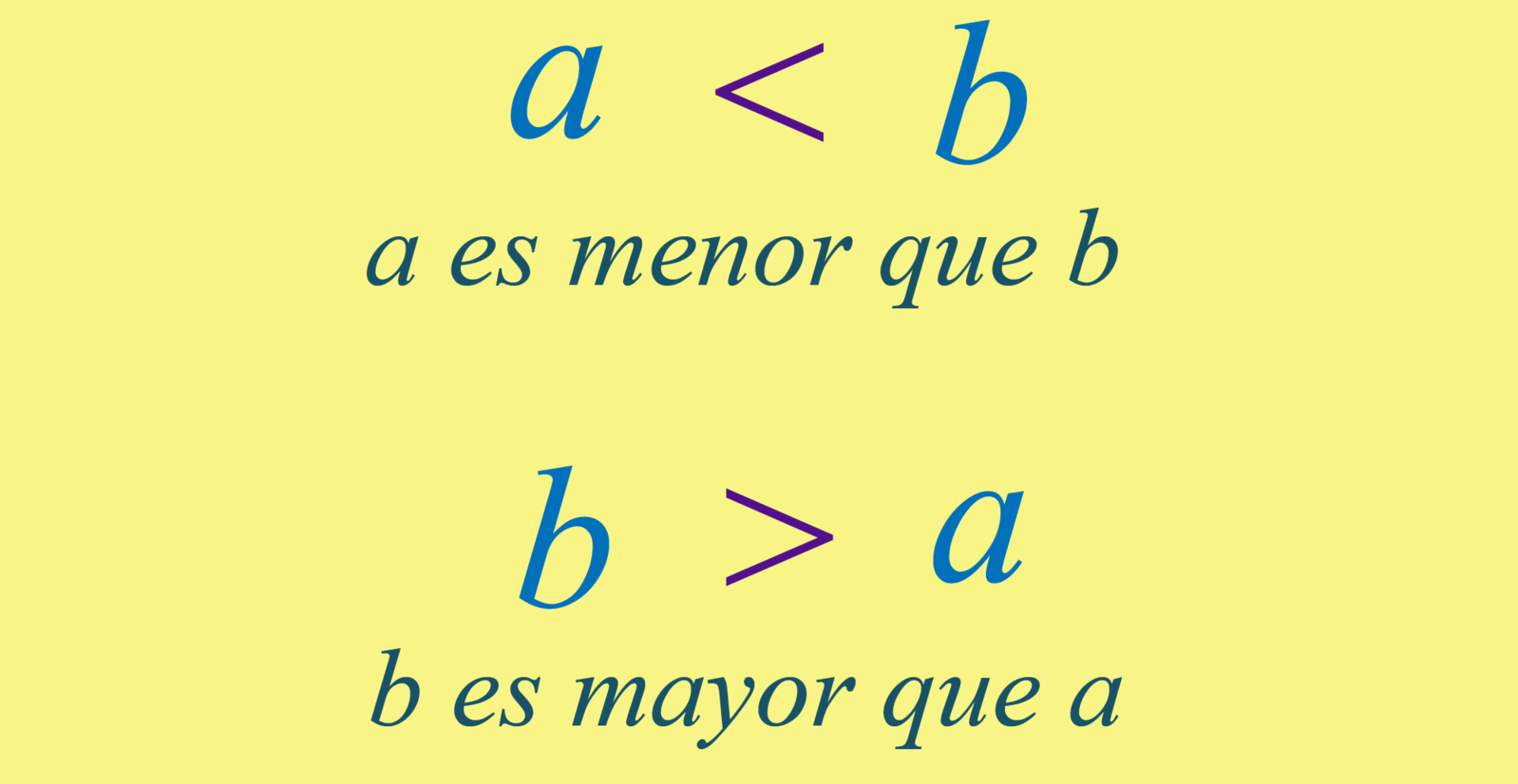
También usamos el símbolo , que es leído como “menor que”. Podemos entonces representar la relación así: que debe ser leída como “tres es menor que cinco”. Una forma práctica de recordar cómo escribir estas relaciones es recordar una pequeña historia: al comienzo, el pez grande siempre iba en persecución de los pequeños... Pero los peces pequeños se unieron y ahora todos juntos van al acecho del pez grande. Por esta razón la boca del signo siempre va dirigida al pez más grande:

Podemos unir varias relaciones de mayor y menor de la siguiente manera: sabemos que y . Podemos escribir expresando no solamente las dos relaciones anteriores, además se da a entender que .


